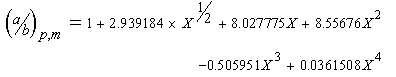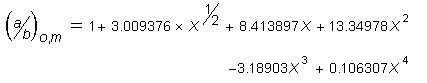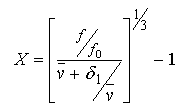Calculating Ellipsoid Asymmetry
The maximum axial ratio of the prolate ellipsoid of revolution (a/b)p,max and the oblate ellipsoid of revolution (a/b)o,max can be determined using a power series approximation of the tabulated data for a/b as a function of f/f0. (Ref. 18) In Sednterp, the coefficients of the corresponding power series in describing a/b were determined using nonlinear least squares analysis (Ref. 46). For the prolate case:
Equation 31:
and for the oblate case:
Equation 32:
(note that the coefficients in both of these equations differ from those in Ref. 59); these values give better accuracy
Over the range 1 <= (a/b) <= 200, these functions are within 0.01 of the true axial ratio and certainly introduce no error beyond that in estimating s0 or f0. Should an estimate of the degree of hydration be available, the corresponding values for and are calculated from equations 31 and 32 using equation 35 for X: Equation 35:
where δ1 is the degree of hydration expressed as g-water/g-protein, vbar is the partial specific volume of the protein and f/f0 is the ratio of the experimentally determined frictional coefficient to that for the equivalent anhydrous sphere (both at 20 C). Again, Teller's empirical estimates (Ref. 33) for and his estimate of Vp = 0.7654 ml/g can be substituted for f0 and vbar in this calculation.